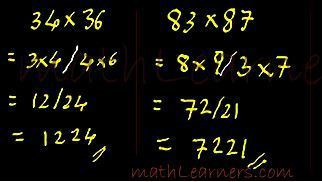Multiplication in Vedic Mathematics

Tirthaji Maharaj has classified tricks to Multiply Numbers in Vedic Mathematics in Specific and General Methods. Specific Multiplication Methods can be applied when numbers satisfy certain conditions like both numbers closer to 100 or numbers closer to each other or addition of last digits of both numbers is 10, etc. While General Multiplication Methods can be applied to any types of numbers.

Depending on Specific and General Techniques, Multiplication in Vedic Mathematics are classified in the form of Sutras as below. Lets see the  Vedic Mathematics Multiplication techniques.

1. Nikhilam Sutra (Specific Technique)
2. Anurupyena Sutra (Specific Technique)
3. Urdhva Tiryak Sutra and Vinculum Process (General Technique)
4. Ekayunena Purvena (Specific Technique)
5. Antyaordaske’pi (Specific Technique)

Nikhilam Sutra:

This is most simplest trick to multiply numbers using Vedic Mathematics. I personally like this method a lot as multiplication can be done in mind as well.

Using Nikhilam Sutra it is simpler to multiply numbers like 98 & 95, 997 & 987, 102 & 112, 995 & 1008 i.e. the numbers which are closer to power of 10.  This Sutra is a Specific method of Multiplication in Vedic Mathematics which shows shortcuts to multiply numbers which are closer to power of 10 (10, 100, 1000, etc. )

This will generate 3 cases:

• Numbers closer and less than power of 10. Example: 97 * 96, 994 * 992, etc
• Numbers closer and greater than power of 10. Example: 102* 108, 1004 * 1012, etc
• Numbers closer and lying on both sides of power of 10. Example: 102* 95, 1004 * 991, etc

Let’s see few examples on this:

Click Here To Check  Process, Types and Examples on Nikhilam Sutra

Anurupyena Sutra:

This is a sub-type of Nikhilam Sutra and another vedic math multiplication trick when numbers are not closer to power of 10 but are closer to themselves. It works on concept of Working Baseand then apply Nikhilam Sutra.

For Example – Multiplication of Numbers like  63 & 67.

Process:

1. Working Base(W.B.) concept: As the numbers (63 & 67) are closer to 60, we take working base as 60 (6*10) instead of 100, here factor is 6.
2. Apply concept of Nikhilam as discussed previously i.e. 63 is 3 greater than 60 and 67 is 7 greater than 60
3. Multiply 3 and 7 to get 21 in 2nd compartment. As base is *10, thus we need to have only 1 digit in 2nd compartment and hence need to carry forward 2 to 1st compartment.
4. Like Nikhilam Sutra, Cross Addition of 63 & 7 or 67 & 3 gives 70.
5. In Anurupyena Sutra, before adding carry forward directly to 1st compartment we need to multiply by the factor (6) and then add the carry forward. This Carry Forward (2) is added to 420
6. Final Answer: 4221

Same multiplication 63 and 67 can be solved by considering Working Base of 70 (10 * 7) as below.

Click Here  To understand the Process and More Examples of Anurupyena Sutra

Urdhva Tiryak Sutra:

This is another great shortcut method of multiplication using Vedic Mathematics. Urdhva Tiryak is General method of multiplication in Vedic Maths which provides shortcut to multiply any types of numbers.

It can be applied very easily to multiply 3 digit numbers, multiply 4 digits numbers and even more than 4 digit numbers.

Lets see an example Multiplication of 3 digit numbers:

Formula Used:  (ax2+bx+c)(dx2+ex+f) = adx4 + (ae+bd)x3 + (af+be+cd)x2 + (bf+ce)x + cf

Process: (Left –> Right)

1. Vertical Multiplication of 1st digits of 2 numbers.
2. Crosswise Multiplication Addition of 1st 2 digits 2 numbers. (i.e. Crosswise Multiplication of 1st 2 digits and adding them.)
3. Crosswise Multiplication Addition of all 3 digits of both the numbers.
4. Crosswise Multiplication Addition of last 2 digits 2 numbers.
5. Vertical Multiplication of last digits 2 numbers.
6. For all steps, except 1st step, each compartment needs to have ONLY 1 digits. If not then carry forward initial digits to previous compartment (Check below examples to understand).

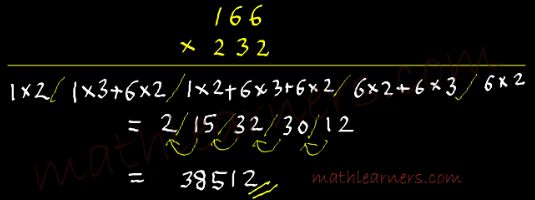
Click Here to Check Process, Multiplication of 4 & more examples using UrdhvaTiryak Sutra.

Vinculum Process of Multiplication: �

Vinculum is a special method of Vedic Maths Multiplication which is used with Urdhva Tiryak whenever we have bigger digits like 6,7,8 and 9.

Vinculum is a process applied when numbers have bigger digits like 6,7,8,9. Carrying out operations like multiplication with bigger digits is time consuming and little tougher as compared to smaller digits. Hence such digits 6,7,8 and 9 are converted to smaller digits like 4,3,2 and 1 using Vinculum Process.

I highly recommend to go through the� concept of Vinculum Process.

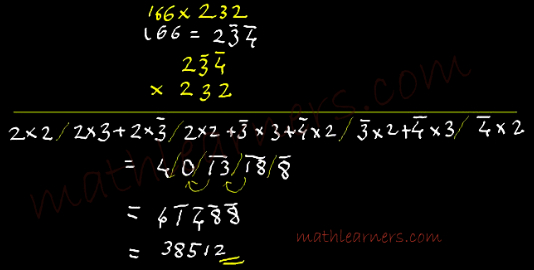
Ekayunena Purvena Sutra:

This sutra is applicable whenever multiplier has only 9’s as digits.

Example:

Click Here => To understand the Process and more examples on Ekayunena Purvena Sutra.

Antyaordasake’pi:

This sutra has another great multiplication trick in Vedic Mathematics which can be applied when last digits of both numbers totals as 10.

Steps:

1. Check if addition of last digits of the numbers is 10.
2. If yes, multiply them and write in 2nd compartment.
3. Apply Ekadhikena Purvena for the remaining digits i.e. Add 1 to the remaining digits.
4. Eg: In case of 34 x 36, Apply Ekadhikena Purvena on 3 so we have 4. Now multiply 3 and 4 and write in the 1st compartment.

What is Vedic Mathematics?

Vedic Mathematics is the name given to the ancient system of Indian Mathematics which was rediscovered from the Vedas between 1911 and 1918 by Sri Bharati Krsna Tirthaji (1884-1960). According to his research all of mathematics is based on sixteen Sutras, or word-formulae. For example, 'Vertically and Crosswise` is one of these Sutras. These formulae describe the way the mind naturally works and are therefore a great help in directing the student to the appropriate method of solution.

Perhaps the most striking feature of the Vedic system is its coherence. Instead of a hotch-potch of unrelated techniques the whole system is beautifully interrelated and unified: the general multiplication method, for example, is easily reversed to allow one-line divisions and the simple squaring method can be reversed to give one-line square roots. And these are all easily understood. This unifying quality is very satisfying, it makes mathematics easy and enjoyable and encourages innovation.

In the Vedic system 'difficult' problems or huge sums can often be solved immediately by the Vedic method. These striking and beautiful methods are just a part of a complete system of mathematics which is far more systematic than the modern 'system'. Vedic Mathematics manifests the coherent and unified structure of mathematics and the methods are complementary, direct and easy.

The simplicity of Vedic Mathematics means that calculations can be carried out mentally (though the methods can also be written down). There are many advantages in using a flexible, mental system. Pupils can invent their own methods, they are not limited to the one 'correct' method. This leads to more creative, interested and intelligent pupils.

Interest in the Vedic system is growing in education where mathematics teachers are looking for something better and finding the Vedic system is the answer. Research is being carried out in many areas including the effects of learning Vedic Maths on children; developing new, powerful but easy applications of the Vedic Sutras in geometry, calculus, computing etc.

But the real beauty and effectiveness of Vedic Mathematics cannot be fully appreciated without actually practising the system. One can then see that it is perhaps the most refined and efficient mathematical system possible.

My First Post